Fundamentación Teórica

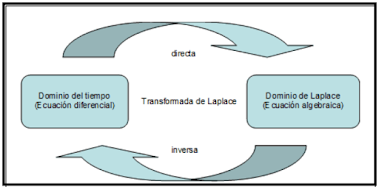
Definición de la Transformada de Laplace 

 Sea f una función definida para valores de $$t\leq 0$$ La transformada de Laplace de f(t) se define como $$L\left \{ f(t) \right \}=\int_{0}^{\infty }f(t) e^{-st}dt$$

- La letra s representa una nueva variable, que para el proceso de integracion se considera constante

- La transformada de Laplace convierte una funcion en t en una funcion en la variable s

- Condiciones para la existencia de la transformada de una función:

1. De orden exponencial

2. Continua a trozos

EJEMPLO

Propiedades de la Transformada de Laplace

Linealidad $$L\left \{ af(t)+bg(t)\right \}=a L{f(t)}+bL{g(t)}$$ Cambio de Escala en el Tiempo $$L\left \{ f(ct) \right \}= \frac{1\frac{}{}}{c}F(\frac{s\frac{}{}}{c})$$ Diferenciación en la imagen $$L\left \{t^{n}f(t) \right \}= (-1)^{n}\frac{d^{n}}{ds^{n}}\left \{ F(s) \right \}$$ Primer teorema de traslación $$L\left \{e^{at}f(t) \right \}=F(s-a)$$ Segundo teorema de traslación $$L\left \{f(t) u_{a} \right \}= e^{-as}L\left \{f(t+a) \right \}$$ Teorema de Division para t $$L\left \{\frac{f(t)}{t} \right \}= \lim_{b \to \infty }\int_{s}^{b}F(u)du$$ Teorema de la transformada de la derivada $$L\left \{f''(t) \right \}= sL\left \{f(t) \right \}-sf(0)-f'(0)$$ Teorema de la transformada de la integral $$L\left \{\int_{0}^{t}f(t)dt \right \}= \frac{1}{s} L\left \{f(t) \right \}$$ Teorema de la Convolucion $$L\left \{ f(t)*g(t) \right \}= L\left \{f(t) \right \} L\left \{g(t) \right \}$$

EJEMPLOS DE CADA PROPIEDAD

Definición de la Transformada Inversa  de Laplace 

La Transformada inversa de una función en s, digamos F(s) es una función de t cuya transformada es precisamente F(s), es decir

$$L^{-1}\left \{F(s) \right \}= f(t)$$

A continuación se mostrará un documento donde se encuentra cada una de la propiedades de la Transformada Inversa de Laplace asi como un respectivo ejemplo de cada , las propiedades de la transformada inversa de Laplace son similares a las propiedades de la transformada Laplace.

Tabla de  Transformadas  de Laplace